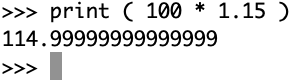私が苦手なもののひとつが、メキシカン料理。

豆をペースト状にしたようなものが苦手です。

しかし、社員にはメキシカン料理が大好きという人たちも多くいて、サンシャイン６０からメキシカンのお店がなくなってがっかりしていました。

10月の誕生会では、そんな気配を察してか、幹事のI君が、メキシカンのケータリングという未だかつて誰も挑戦したことのない領域に踏み出したのです。

今回利用したお店は、SALSA CABANAです。都内唯一のメキシカンケータリングとのこと。

こんな感じになりました。

気がつくと、豆料理がない！

これは助かったと思いながら食べてみると、とても美味しかったです。

わざわざ小さなソンブレロと付け髭で場を盛り上げた幹事、ごくろうさまでした。

当社のシリコンバレーインターンシップで2年にわたり作ったボランティアマッチングシステム　SOVOLというものがあります。

SOVOL
https://sovol.earth

これは、

個人がボランティア募集して、

個人が応募する

ということができるもので、台風被害のように、片付けを手伝って欲しい時などはとても役に立ちます。

市役所ボランティアセンターはいまだ開設しておらず、一番人手が欲しい時に募集できません。

また、集合場所が市役所に9時、そこでボランティア受付に1時間、行き先を割り振られて、実際に現場に行って作業開始は11時などになってしまうのに対して、SOVOLならば朝9時に現場に行くことが可能です。

SOVOLは運用開始後、たまに利用者がいる程度で現在も利用がありませんが、こういう時に利用してもらえればと思い、ここに記載させていただくとともに、社会貢献活動として当社も行っていますが、予算もかけて宣伝していこうと考えています。

しかしながら、どう宣伝したらいいか、いいアイデアもないため、もしよろしければ、こちらのコメント欄にアイデアを記載いただければ幸いです。

コメントは匿名希望と書いてある場合は公開しませんので、お気軽にいただければ幸いです。

消費税10%で大きな問題も起きず、一安心しているシステム管理者も多いことでしょう。私もその一人です。

さて、これまで

３％　→  ５％　→ ８％　→ １０％

と上がってきた消費税ですが、今後、もし１５％になると、これまで起きなかった問題が起きることが予想されます。

それは…………………………

コンピュータの計算が狂う

のです。

百円のものに１５％の消費税がかかるという計算を、コンピュータで普通にやってみます。ここでは Macの Pythonというプログラミング言語でやった例を表示します。

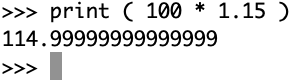
「＊」はかけ算の意味です。

消費税は、一般的に切り捨て（*1）となるので、百円のものを買えば115円になるはずが、114円になってしまうという計算結果になるのです！

どうしてこんなことが起きるのでしょう？

それは、コンピュータは内部では２進数を使っていて、小数点以下の数字は２進数で正確に表せないことが多いから、なのです。

「え？！　どんな数でも２進数で表せるよね？」

と思われる方も多いでしょう。整数においてはそうなのです。

１０進数で表される小数点以下の数が他のN進数で表せないということを感覚的に理解してもらうために、３進数を考えてみることにします。

３進数は３つ集まると桁があがります。

１、２の次は３ではなく、１０になり、その後は、１１、１２となって、その次は２０になります。

使われる数字は０、１、２の３つです。

では３進数の０．１はどういう数でしょう？

０．１が３つ集まったら桁があがるので、１になります。

ということは、３進数の０．１は１０進数で言えば、１を３で割った数で、０.３３３３３……になり、どこかで桁を切らざるを得ず、微妙な誤差が出てしまいます。

この例では、３進数→１０進数で誤差がでるという話ですが、同様なことが１０進数→２進数でもあって、お互いに小数点以下の数は誤差がでることが多いのです。

では、なぜこれまでの３％、５％、８％、そして今回の１０％の時に起きなかったのでしょう？

理由は簡単で、「２進数の値が、ほんのすこし大きかった」からです。ほんの少し大きい数をかけて、最後に切り捨てにするので問題になりませんでした。

下の表の、１．０３、１．０５、１．０８、１．１０のコンピュータ内部の数を見てください。いずれもすこし大きくなっています。

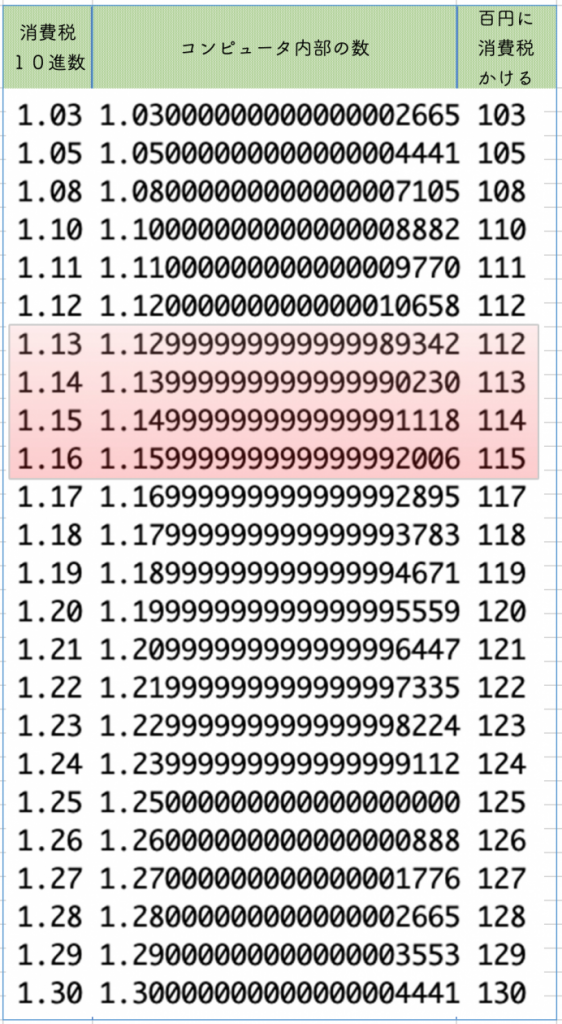
それに対して、消費税１３％から消費税１６％については、ほんの少し小さくなります。それが原因で百円の消費税が１円少なくなってしまうのです。

念のため、百円のものに対する消費税を３０％まで誤差を計算してみたところ、消費税１３％から１６％の時に、誤差が出ることがわかりました。

面白いのが、値段によって誤差が出る時とでないときがあります。

たとえば、３００円のもので計算すると、誤差がでないのに、４００円だと誤差がでます。

買い物をする側にとっては１円トクをする話です。

ただし、これにはちゃんと対策があって、整数計算にする方法がその一つです。

つまり　１００ × １．１５を計算するのではなく

１００　× 　１１５　÷　１００

というふうに整数計算にしてしまう方法や、精度の高いライブラリを使うなど、いくつか対策があります。

１５％の消費税の時に、対策をしていないと１００円の商品に対して１４円の消費税になることが予想され、しかも値段によって正しい答えが出たりするので混乱しそうです。

（*１）消費税に端数が出た場合は、切り捨て以外の方法も法的には可能なようですが、ほとんどのお店では切り捨てにしています。