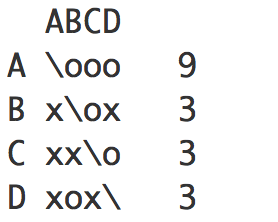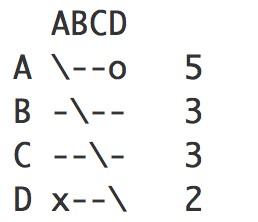社内においてある自販機は、全品50円大特価になっています。
昨日、自販機の定期補充の方が来て、補充していたのですが、なんと、自販機が当たりつきにバージョンアップしていました。
買うたびに、ピピピピッピ、と音がなり、いつもは投入した金額を表示するところが回転して、４つの数字が並びます。
そして、本日昼休み、初めての大当たりが出ました。（写真上）
記念すべき大当たりは、技術部Y君。
「おおお、すごい、記念に写真撮るから、待ってて」
と写真を撮っていたら…
「４４４４」の表示が消え、ボタンのところのライトも消え、せっかくの大当たりが無効になってしまったのです。
＜＜教訓＞＞
幸運の女神には前髪しかない。訪れた瞬間に前髪をつかまないと通りすぎてしまう。チャンスがやってきたら、逃さずつかまないといけない。
＊本エントリは2018年W杯初戦勝利の時点で書いたものですが、2022年W,杯でも初戦勝利となりましたので、同様の計算が成り立ちます。(2022/11/24追記)
サッカーW杯のグループリーグは、４チームが総当たりで、勝ち＝勝点３、引き分け＝勝点１、負け＝勝点０となって、その勝点でグループリーグ順位が決まります。
全部で何通りあるかというと、全６試合で勝ち、引き分け、負けの３パターンなので、
３の６乗 ＝ 729通り
あるわけです。
さびついたプログラミング能力ですが久々にC言語を使って、全729通りを分析してみました。
現在、日本の勝点は３ですが、あと２試合負けて勝点３のままだと、
１）勝点３で同点にならずに突破するのは、12パターンです。
３引き分けで勝点３の時のみ、同点にならずにグループリーグ突破することがあります。日本チームは、１勝したため、このパターンにはなりません。
全12パターンは、こちら。
２）勝点３で並ぶパターンは、21パターン。
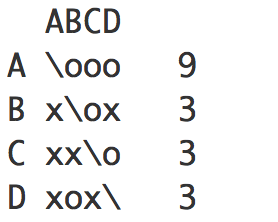
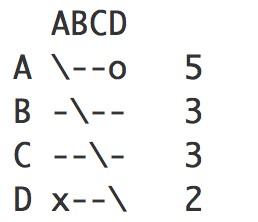
上記のようなパターンです。
１勝２敗で３チームが並ぶパターンと、
３引き分けで２チームもしくは全チームが並ぶパターン。
全21パターンはこちら。
３）勝点３で同点にならず敗退となるパターンは、320パターン
よって、勝点３のままでグループリーグ突破は難しいが、不可能ではないことがわかります。ただし、同点にならずに突破するのは、全試合引き分けのみです。
勝点４（１勝１敗１引き分け）の場合は、
１）勝点４で同点にならずに突破 168パターン
２）勝点４で並ぶ 170パターン
３）勝点４で同点にならずに敗退 120パターン
おお、なんと、日本はあと１試合引き分ければ、かなりの確率で突破できそうです。
同様に勝点５、６で計算すると
勝点５（１勝２引き分け）
１）突破 252パターン
２）並ぶ 4パターン
３）敗退 ゼロ
勝点６（２勝１敗）
１）突破 252パターン
２）並ぶ 8パターン
３）敗退 ゼロ
面白いことに、勝点５と勝点６だと勝点５の方が並ぶパターンが減る分、若干良さそうです。
（念のためですが、勝点５、６で敗退ゼロの意味は、勝点だけで敗退することがない、という意味です。勝点が同点で並んだ中で、得失点差等で敗退する可能性はあります。）
正確を期したつもりですが、さびついたプログラミング能力のため、もしかしたらミスがあるかも知れません。お気付きの方はコメントでお知らせください。コメント非公開ご希望の方は、その旨、お書き添えください。
また、タイトルが確率を計算してみた、となっていますが、実際には確率計算に必要な順列組み合わせを計算しました。この数字から簡単に確率は計算できるのですが、単なる数値的な確率を出すことは、全身全霊で戦っている日本チームに対して失礼であると考え、確率ではなくあくまでパターン数を出すに留めました。
この6月10日で57歳になりました。
サザエさんのお父さんの波平さんは54歳ですから、もう３つも年上になってしまいました。
さて、恒例の誕生会ですが、基本、私はリクエストをしないことにしています。が、今回は、「たまには叙々苑とか、外で食べたい」と言ってしまい、幹事が忖度して（はっきり店の名前まで言ってますから、忖度ではないですね）叙々苑になりました。
小雨の中、5,6分歩いて叙々苑まで行き、大変おいしくいただきました。
DOSHというアプリがあります。
買い物をすると、キャッシュバックが貯まっていくというものです。
テキサスのスタートアップが運営しています。
スマホアプリのみの提供なのですが、そのURLが
なんです。
DOSH（ドッシュ）だけだと、なにそれ？という感じですが、
「ドッシュ（ドット）キャッシュ」になると、にわかに
なに？お金の話？？
という感じで、食いつきがよくなりそうですね。
非常にうまく、.cashドメインを利用した例だと思います。
「.cash」はゴンベエドメインでオンラインで取得可能です。
どうぞキャッシュに関係しそうなサービスやコンテンツにご利用ください。
参考：Austin company with $57 million in funding uses .CASH domain
先日の卓球ジャパンオープン男子シングルスで張本智和選手が優勝しました。
動画開始２秒くらいで、「GoDaddy SSL証書」（実際には簡体字）という文字が床に書かれています。
GoDaddy社は、ドメイン登録数が2005年より世界１位、SSL証明書の販売数が世界２位の会社です。（Wikipedia）
２０１６年から卓球のWorld Cupにスポンサーを開始し、２０１７年は５大会に、そして２０１８年には１２大会にスポンサーする予定になっています。
上の写真は、Wikipediaに掲載されているもので、2017年のドイツ大会の上田仁選手です。
ちょうど上田選手の後ろに、「GoDaddy 買域名」（実際は簡体字）とあります。意味は、「ドメイン名を買おう」です。
2017年頃までは、ドメイン名販売を宣伝していたのが、張本選手の優勝したジャパンオープンではSSL証明書の宣伝になっていて、若干、方向性を変えたようですね。
GoDaddy社のアジア太平洋担当副社長のロジャー チェン氏によれば、卓球はアジアで長年人気のあるスポーツで、GoDaddyの宣伝にとても役立っているとのことです。
最近、私は卓球を40年ぶりに再開しました。GoDaddy社のようなスポンサーはできませんが、日本チームは心から応援しています。
午前は、まず立川へ。
代理店のセキド社が、まだ発売前の水中ドローンを見せてくれるというので見に行きました。
クラウドファンディングの商品開発は、なかなか成功しませんが、これはとてもうまくいったようで、性能も申し分なしでした。
実際には、室内にあるプールで操縦したのですが、こんな感じ。
まだ発売前なので、予約注文をしました。
午後は、横浜市金沢区のSEKIDO DJI ドローンフィールドへ。
立川から約２時間！
空のドローンの初心者講習会 New Pilot Experience です。
最新の機種含め、DJIの３機種を体験できました。
うーん、ファントム3の頃より、いろいろ進化していますね。
体験のあとは、１時間弱の座学です。と言ってもビデオを見たり、パワーポイントの資料を説明してもらいました。
今後、海と空のドローンにいろいろと活躍してもらおうと思っています。なにに使うかは、お楽しみ、ということで。
【2018/7/6追記】本ブログで絶賛したアマゾンダッシュボタンですが、ちょっと残念なことがあり、「アマゾンダッシュボタンの残念な話」に記載しました。
今日はアマゾンの宣伝になってしまうのですが…
アマゾンダッシュボタンというものがあります。
たとえば、上の「サントリー天然水」ダッシュボタンは、ボタンを押すと、サントリー天然水がおうちに届く、というものです。
これを、私の家では冷蔵庫に貼っています。（マグネットがついていて貼れます）
あと、エリエールダッシュボタンをトイレに貼っています。
水がなくなったり、トイレットペーパーがなくなったら、これを押すと、翌日には届くわけです。
Amazon Prime会員でもあるので、送料無料です。
これがどういう時に役立つかというと、
「私が出張でいない時でも、母がボタンを押すだけでいい」
ということなんですね。
これ、高齢のご両親がいる方など、実家に設置すると、ほんと便利なのでおすすめです。
ひとり暮らしのお年寄りでも、わざわざ重いものを買いに行かずに、インターネット通販同等のことができるわけです。
初期設定で配送先や配送商品、Wifiの設定をアマゾンアカウントを持っている人が最初にやる必要があります。
ダッシュボタンは500円ですが、初回注文時に500円分値引きされるので、実質無料です。
いいことばかりのようですが、デメリットは、
日時指定できないので、留守がちのお家には不向き
押したつもりが押せてないときがあった
くらいでしょうか。押すと、アマゾンアカウント所有者には連絡が来ます。さらに、２回連続で押しても、最初の注文が到着するまでは、無効化されるので、家族がトイレに入るたびトイレットペーパーを注文しても届くのは１回だけで、家の中がトイレットペーパーで溢れる心配はありません。
アマゾン以外でもこのパターンはありえると思うのですが、たとえば、
ピザ宅配ダッシュボタン
宅配寿司ダッシュボタン
とかあればいいのに、と思います。
なにがすごいか、というと、デジタルデバイドを解消するアイテムだということです。デジタルに詳しくない人でもデジタルのメリットが（完全ではありませんが、一部）享受できるアイテムです。
あと、改善してほしいことですが、バーチャルダッシュボタンを、アマゾンアプリからでなく、アプリのような扱いにして、スマホからワンタッチで注文できたらいいのにと思います。
